#Euler’s theorem and generalization

[positively-knotted]

Euler Class and Euler Characteristic

This is a follow-up to this post from November. Or more of a redo - I really didn't like how that turned out. Way too detail-focussed, and it didn't even get to the Euler characteristic.

So, this time, we'll take a different tack. As a reminder, here's the idea. Take a smooth closed m-manifold M. Often, if there's some property of M, we like to rephrase it as a property of the tangent bundle TM, and then see if it generalises to other vector bundles, like you can do for orientation. The aim here is to do that for the Euler characteristic.

Prerequisites: being comfortable enough with homology and cohomology, and e.g. sections of vector bundles. I think the most hard-core anything really gets is Poincare(-Lefschetz) duality, and the Kunneth theorem. In particular, I write the Kunneth pairing on cohomology H*(X)⊗H*(Y) -> H*(X×Y) as (a,b) -> a×b. Prewarning that this is fairly long.

Motivating Examples

Let's just take the easiest examples: S¹, S², and S³. Χ(S¹) = χ(S³) = 0, while χ(S²) = 2. What else is non-trivial in the S² case? The tangent bundle! In fact, it's a nice exercise to see that (by stereographic projection on fibres), TS² = S²×S² \ Δ, where Δ is the diagonal. Is there an easy way to see where the 2 comes from? Well, think about sections, i.e. vector fields. Both S¹ and S³ have non-zero sections - in particular, a generic section has 0 signed intersection number with the zero-section. The algtop student's favourite result, the hairy ball theorem, says that this isn't true for S². In fact, a generic section meets the zero section twice, or a generic vector field has two zeros, at the two "tufts of hair".

So we conjecture: the Euler characteristic is the number of signed intersections of a generic section with the zero section. In fact, it's a classical (?) theorem that a closed manifold M has a non-zero vector field iff χ(M) = 0. But we won't assume this.

Algebraifying and Generalising

The standard definition of the Euler characteristic as the alternating sum of ranks of (co)homology suggests that we want to codify this in terms of algebraic topology. So let's do that. Writing s : S² -> TS² for the generic section, and 0 for the zero section, [s⁻¹(0)] ∈ H₀(M;Z) is the signed number of self-intersections, up to some choice of generator. To help fix a generator, we need an orientation. Thus, we'll pass to a generic coefficient ring R, and assume M is R-oriented, with fundamental class [M]. To actually get a honest-to-god element of R, we actually define the Euler class e(M;R) ∈ Hᵐ(M;R) to be the Poincare dual of [s⁻¹(0)]. Then our conjecture is that the R-valued Euler characteristic χ(M;R) is the Kronecker pairing ⟨e(M;R), [M]⟩ of the Euler class. I'm gonna stop writing coefficients now.

But wait! This definition already didn't depend on our choice of vector bundle. If E -> M is any rank-m vector bundle, [s⁻¹(0)] ∈ H₀(M) is (almost) the number of signed intersections of s with the zero-section, and we can define e(E) ∈ Hᵐ(M) to be the Euler class of E. Then maybe we can ask what ⟨e(E), [M]⟩ is telling us. At the end, we'll also define it for arbitrary rank, but that's a little harder at this point.

The Thom Class, sort of

[s⁻¹(0)] is a bit of a pain algebraically. But actually so are vector bundles: since E deformation retracts onto M, we can't distinguish between vector bundles using homology. Instead, the standard trick is as follows. By choosing some metric, we can construct the disc bundle D(E), which is just the unit disc in each fibre. This is now compact, with boundary the sphere bundle S(E). And although the homology of D(E) only depends on M, the homology of the pair (D(E), S(E)) actually does depend on E! Exercise: if M = S¹ and E is the trivial bundle, show that D(E)/S(E) is homotopy equivalent to the wedge sum S¹ v S²; if E is the non-trivial bundle, then D(E)/S(E) is RP².

Ok, so let π : D(E) -> M be the projection, and let u' = π* e(E) ∈ Hᵐ(D(E)). Abuse notation and view M as a subspace of D(E) by the zero section, and let u ∈ Hᵐ(D(E),S(E)) be Poincare dual to [M]. Equivalently, since all sections are homotopic, u is Poincare dual to any section.

Then [s⁻¹(0)] = π_∗( [M ∩ s(M)]). Intersection is Poincare dual to the cup product, so

[M ∩ s(M)] = (u ⌣ u) ⌢ [D(E),S(E)] = u ⌢ [M,S(E)].

Alternatively, naturality of the cap product says that

[s⁻¹(0)] = e(E) ⌢ [M] = π_∗ ( u' ⌢ [M] ).

But since π_∗ is an isomorphism, as is capping with [M] or [M,S(E)], we get that u' is just the restriction of u. (If you're not super comfortable with relative classes, this is basically saying that u' is the "absolute" and u is the "rel boundary" version of the same thing.) This class u is called the Thom class of the vector bundle.

To summarise so far: if u is Poincare dual in D(E) to the zero section, and e(E) is Poincare dual in M to the preimage s⁻¹(0) of the zeros of a generic section, then the restriction u' ∈ Hᵐ(D(E)) is the same as the pullback π* e(E). Maybe this isn't super exciting, but u and u' seem easier to work with then e(E) does.

The Thom Isomorphism, sort of

This is very much not the usual construction of the Thom class, since it relies on Poincare(-Lefschetz) duality, so on the base space of the bundle being a closed manifold. In fact, the Thom class exists for any R-oriented vector bundle on an arbitrary CW complex (or even paracompact topological space!). There, it is usually defined as the unique class in Hᵐ(D(E),S(E)) such that, when restricting to each fibre, the it gives the R-orientation.

Let's show that such a class v exists. The previous post does it in detail, but the basic idea is that a CW structure of M induces one on D(E)/S(E), with one (i+m)-cell for each i-cell in M, and an extra 0-cell coming from the point S(E)/S(E). Then for any point in M, we can choose it to be a 0-cell, and if M is connected, the only 0-cell. So Hᵐ(D(E),S(E)) = R, and it is generated by something that generates the orientation over that point. But the point was arbitrary, so the generator restricts to the R-orientation on any fibre. We then choose v to be the generator.

The main point for us is that we have the following isomorphisms:

R = H⁰(M) -> Hᵐ(D(E),S(E)) -> Hₘ(D(E)) -> Hₘ(M).

This takes 1 to the Thom class v, then to the Poincare dual of v, then to some generator, which by following orientations is [M]. In particular, the Thom class v is exactly what we called u earlier! Thus u isn't just the Poincare dual of the zero section, it's also the unique class that restricts on fibres to give the orientation.

Diagonal Maps Are Often Useful

This next step might seem like it's coming out of nowhere, but it's a super useful trick that you almost certainly will see again. Let ∆ : M -> M×M be the diagonal map. Then TM is canonically isomorphic to the normal bundle NM by (x,v) -> ((x,x),(v,-v)). So we might as well think about e(NM) rather than e(M). For notational ease, I'll write E for some open tubular neighbourhood of Δ(M), thought of as the normal bundle. Then D(E) is just some smaller closed tubular neighbourhood, and Hᵐ(D(E),S(E)) = Hᵐ(M×M, M×M\∆) by excision. Restricting again to Hᵐ(M×M), write u'' for the image of the Thom class. Now e(M) = e(E) = ∆*(u''), so if we can understand u'', we should be ok.

The Slant Product, sort of

Instinctively, u'' is symmetric about the diagonal. Rigorously, this means that (1×α) ⌣ u'' = (α×1) ⌣ u'' for any cohomology class α ∈ H*(M). To prove this, basically observe that the two projections M×M -> M agree on the diagonal, so are homotopic on a small tubular neighbourhood, so induce the same map on cohomology. I'll leave the details as an exercise. So to compute u'', it might be useful to look at something that breaks the symmetry.

We have one map H*(M×M) -> H*(M), by ∆*. But this treats both components the same - can we find one that treats them differently? Sure! We can define μ: H*(M×M) -> H*(M) as follows. If φ ∈ Hʲ⁺ᵐ(M×M), then μ(φ) evaluates on simplices by eʲ -> φ(eʲ×[M]). For lower rank, μ(φ) = 0. This isn't a ring homomorphism, but it is linear. Two key facts to observe about this: for α ∈ Hʲ(M), β ∈ Hᵐ(M), and γ ∈ Hᵏ(M×M),

μ(α × β)= α ⟨β,[M]⟩ and μ((α × 1) ⌣ γ) = α ⌣ μ(γ).

The first condition captures the asymmetry in the definition; the second is an analogue of being a ring homomorphism.

Intuitively, μ sorta "divides by M on the right", so it seems like a good candidate for something that breaks symmetry. Also, since u'' is kinda just built from one copy of [M], maybe μ(u'')=1?

Field Coefficients

So let's compute! Fix a 0-simplex p. μ(u'') evaluates on it like u'' evaluates on p×[M], which by definition of u'' is how the Thom class u evaluates on the pushforward of p×[M] into Hₘ(M×M, M×M\∆) = Hₘ(D(E),S(E)). But under this pushforward, p×[M] is homologous to the fibre over p, and in a way that agrees with the orientation. Hence u evaluates to 1, since the fibre-restrictions of u generate the orientation. And since it evaluates to 1 on any 0-simplex, it's just 1 ∈ H⁰(M).

Quick recap of what's just happened: first, we moved from e(E) to the Thom class u. Now, we've moved to some symmetric u'' in Hᵐ(M×M), and defined a relatively well-behaved, asymmetric map μ that sends u'' -> 1. The aim will be to use μ to control what u'' can be, and hence what e(E) is.

We're going to assume that R is a field for a moment. This is just so that H*(M×M) = H*(M)⊗H*(M). In particular, for any basis {bᵢ} for H*(M), we can write u'' = Σ bᵢ×cᵢ, for some cᵢ.

Recall that (1×bᵢ) ⌣ u'' = (bᵢ×1) ⌣ u''. I didn't just mention that for no reason - let's apply μ to both sides. On the RHS, we get

μ((bᵢ×1) ⌣ u'') = bᵢ ⌣ μ(u'') = bᵢ.

This makes sense - μ is removing the [M] on the right, and since we know u'' is ~just one copy of [M]~ in some sense, the only thing left is the bᵢ on the left.

On the LHS, it's more complicated, since we're adding things to the right. Expanding, we get

Σ (-1)^{dim bⱼ} μ(bⱼ × (bᵢ ⌣ cⱼ)) = bᵢ.

By considering bases, we get that ⟨bᵢ ⌣ cⱼ, [M]⟩ = (-1)^{dim bⱼ} if i=j, and 0 or undefined otherwise.

Remember that e(M) = ∆*(u'') = ∆*(Σ bᵢ×cᵢ) = Σ bᵢ ⌣ cᵢ. So pairing with [M] gives exactly Σ (-1)^{dim bᵢ} = Σ (-1)ᵏ dim Hᵏ(M) = χ(M). Which is exactly what we wanted! The Euler characteristic is the pairing of the Euler class with the fundamental class.

This can seem almost magical, or in less kind words, unmotivated. But maybe here's another way to think of it. For any basis {bᵢ}, we can construct a dual basis b'ᵢ, such that ⟨bᵢ ⌣ b'ⱼ, [M]⟩ = δᵢⱼ is the Kronecker delta. In the notation above, b'ᵢ = (-1)^{dim bᵢ} cᵢ . Then u'' = Σ (-1)^{dim bᵢ} bᵢ × b'ᵢ. The fact that this sum gives u'' is kind of saying that u'' contains all of M, but is symmetric so also contains the dual. That's my intuition anyway. The fact that it really does just give the Euler characteristic is slightly magical, since it relies on the alternating sum showing up perfectly.

PID Coefficients

For a general PID, we fix this by just passing to the field of fractions. χ(M) is the same, and you can follow through our construction to check that e(M) and [M] are too. So once again, ⟨e(M), [M]⟩ = χ(M). For NON-PAID coefficients Kunneth fails, so it wouldn't surprise me if this failed to. But realistically who cares.

General Vector Bundles

Everything we did here was for rank-m bundles. But all of it basically works for arbitrary rank-k bundles, at least for m≥k. In this case, M ∩ s(M) has dimension m-k, so e(E) ∈ Hᵏ(M). Now it can't really be thought of as a number in any meaningful way, but it's still cool that we can think of it as a generalisation of the Euler characteristic!

For k>m, we just say e(E) = 0, since it ought to live in Hᵏ(M)=0. Slightly disappointing.

What Does e(E) Tell Us?

Here's the most often cited example, and our original motivation. If E admits a non-zero section, then e(E) = 0.

Proof: suppose s : M -> E\M is the section, and write i : E\M -> E for the inclusion. Then πis : M -> M is the identity map. π^*e(E) = u' by definition, so (πi)*e(E) = i* (u') = 0, since u' is the restriction of a relative class. So (πis)*e(E) = e(E) = 0.

You might think this is less helpful than the fact we started with, that a closed manifold M has a non-zero vector field iff χ(M;Z) = 0, since saying e(E) = 0 assumes we have a coefficient ring R such that E is R-oriented, whereas the theorem lets us use integral coefficients. However, nothing like that theorem is true for arbitrary vector bundles (or bundles on general CW complexes), when the Euler class is the best we have. So like all good generalisations, it does lose some information.

[squareallworthy]

It's Triangle Tuesday! A triangle, its centroid, a theorem, and two bonus triangles.

Greetings, seekers of triangle knowledge. Today I'm going to talk about the centroid.

Among triangle centers, the centroid is, at first glance, maybe a bit underwhelming. Take a triangle ABC. Let the midpoints of the sides be M_a, M_b, and M_c. Draw a line from each vertex to the opposite midpoint. The three lines cross at a point G. And that's the centroid.

Very simple. Simple almost to the point of banality. Don't get me wrong - the centroid is a great point. It's just not very flashy in its construction, and the fact that it exists doesn't seem at all deep. Later on, we can show how the centroid relates to other things, such as the symmedian point, the Euler line, and the nine-point circle. But for now, it's kind of hard to appreciate the centroid on it own. Let's do what we can do now, before getting into that other stuff, to see why the centroid is interesting.

It's not at all difficult to prove that the lines meet at one point, but the proofs I've looked at aren't all that enlightening. You draw a line and look at some parallel lines, and you say, "mmm, okay, that checks out, that's a proof all right," but it doesn't feel like you've learned much.

Even before proving that the lines are all coincident, it seems obvious that they should be. Each line cuts the triangle into two equal parts, and so when you draw two of them, the point where they cross is the middle of the triangle, measured two ways. So it just makes sense that the third line has to go through the same point, right?

Let's see if we can follow our intuition on this to get at something more fundamental. The lines that connect the vertices to the midpoints of the side are called medians. In general, lines like this that extend from a vertex to the opposite side of the triangle are called cevians (pronounced ˈtʃeviən, CHAY-vee-un). Are the medians really all that special among other cevians? What if instead of marking the midpoint of each side, dividing it into two segments in a 1:1 ratio, we mark a point that divides the side in a 1:3 ratio, going counterclockwise around the triangle? If we then draw the cevians, what do they look like?

Not surprisingly, the they aren't coincident. They outline a triangle (in red) that looks like the original triangle, but smaller and tilted counterclockwise. If we divided in a 1:3 ratio going clockwise, we would get a clockwise-twisted triangle. And if we move the marked points back and forth, sure enough, only when the points are halfway along the sides do the three cevians cross at one point.

And if we take the crossing point of two cevians, and then draw the third line through that point? Where does that hit the opposite side? Here I'll go back and draw that with a dashed line on the 1:3 ratio counterclockwise drawing:

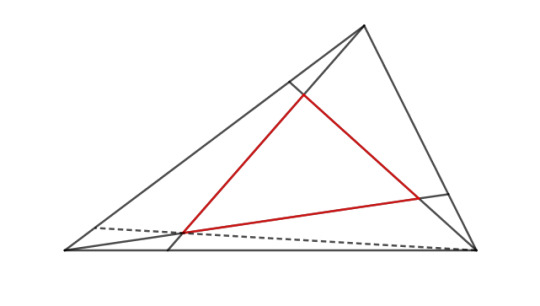
It lands pretty close to the vertex. Somehow that point has to balance the 1:3 ratio we used to measure the other points, but it's not clear exactly how.

So how are coincident points connected to the place where we cut the sides? Let's get a bit more formal. Let's have a triangle ABC, and a point P that is not located on any of the sides of the triangle. We'll draw cevians from the vertices through P, and they will cross the sides of the triangle at D, E, and F.

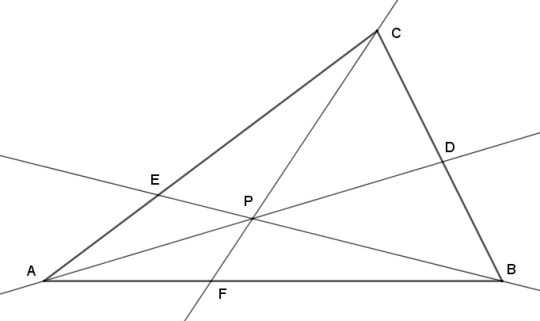
So we would like to know where F, for instance, cuts line AB, and how it relates to the other points. Or, to put it another way, if we knew the ratio of the length of AF to FB, and the same for BD to DC, could we say what the ratio of CE to EA is? Conversely, if we have a triangle with three cevians cutting the sides at D, E, and F, and we knew all the ratios AF/FB, BD/DC, and CE/EA, could we say whether the cevians are coincident or not?

It's easy to get lost here with statements made up of long strings of segments. If you are like me, your eyes start to glaze over when you see that and you don't learn anything. So let's lay out a plan for figuring this out. We are looking for some information about ratios of line segments. To do that, it would be helpful to have some similar triangles, because similar triangles have all the same angles, and differ only in size and orientation. So if you know something about the ratio of two sides of a triangle, you know the same thing about the corresponding sides of a similar triangle.

And a good way to get some similar triangles is to arrange to have them meet vertex-to-vertex between parallel lines, like this:

With this arrangement and a little bit of Euclid (which I won't get into here), we can show that the pairs of angles marked with the same letters are equal. The two triangles with angles α, β, and γ are therefore similar, and we can say that the corresponding sides are in the same proportions -- that is, if we compare the red dashed segment to the blue dashed segment, it is the same ratio as the red solid segment to the blue solid segment. The four colored segments together make a Z-shaped figure, and it is this kind of arrangement of segments that we want to consider as we figure out what's going on with our cevians.

So with that in mind, let's go back to triangle ABC and add a line through A that is parallel to side BC. The new line meets two of our cevians at G and H.

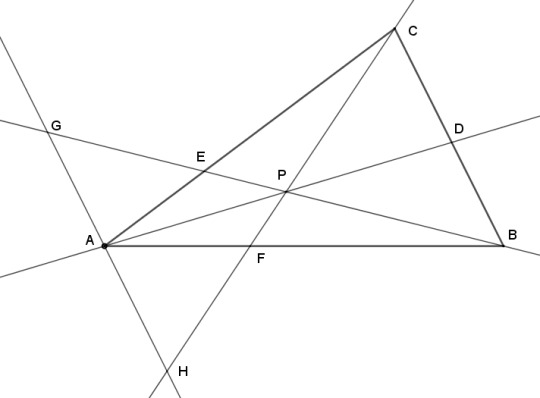
And that creates sets of similar triangles:

AHF is similar to BCF (in red, below)

AEG is similar to BCE (green)

AGP is similar to BDP (blue)

AHP is similar to CDP (yellow)

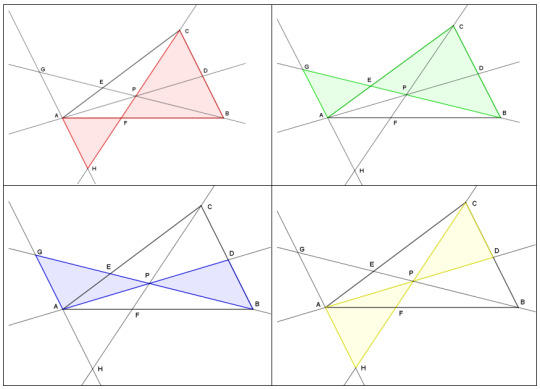
From that, we can get these relationships:

AF/FB = AH/BC (from the red triangles)

CE/EA = BC/AG (green)

AG/BD = AP/DP (blue)

AH/DC = AP/DP (yellow)

We are interested in the ratios that the sides of ABC are divided into, that is, AF/FB and so on. We have two of them above, which I have bolded. We still need to get BD/DC and then shuffle things around to get all of those into one equation.

The two equations above from the blue and yellow triangles have the same right hand side, so we can say

AG/BD = AH/DC

and by reshuffling,

BD/DC = AG/AH.

There's the ratio for the third side. Now let's multiply that together with the equations we got from the red and green triangles:

AF/FB * CE/EA * BD/DC = AH/BC * BC/AG * AG/AH.

Everything on the right cancels out, so if we reorder the things on the left side to be alphabetically nice, we have

AF/FB * BD/DC * CE/EA = 1

which is the first half of what we wanted to know. If three cevians pass through the same point, then they cut the sides into ratios that multiply to 1. What a nice simple relationship to remember!

What about the converse? Can we prove that if three cevians cut the sides in ratios that multiply to 1, they all pass through the same point?

Let's suppose that we have divided the three sides of ABC with points C, D, and E in a way that AF/FB * CE/EA * BD/DC = 1. Then let's draw the cevians BE and CF and say that their crossing-point is called P.

Now, if we draw a cevian from A through P, does it land at D, as our equation says it should? Well, it has to land somewhere, and we'll call that point D'.

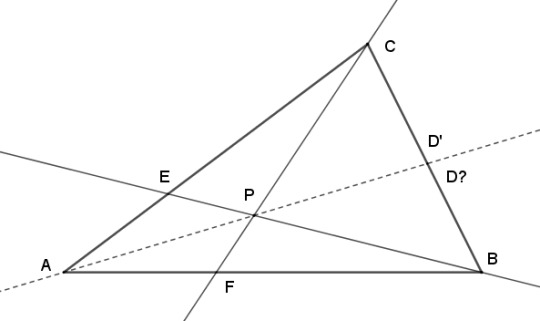
Can we prove that D' = D?

We were given that

AF/FB * BD/DC * CE/EA = 1.

And since we just drew three coincident cevians, we can conclude from what we just proved that

AF/FB * BD'/D'C * CE/EA = 1.

Combining those, we do a little algebraic manipulation:

BD/DC = BD'/D'C

BD/DC + 1 = BD'/D'C + 1

BD/DC + DC/DC = BD'/D'C + D'C/D'C

(BD+DC) / DC = (BD'+D'C) / D'C

But BD+DC is the whole side BC of the triangle, and the same with BD'+D'C. So

BC / DC = BC / D'C

and therefore D = D'. And that's our theorem:

In a triangle ABC, lines connecting the vertices to points on the opposite sides D, E, and F are concurrent if and only if AF/FB * BD/DC * CE/EA = 1

This is called Ceva's theorem, after the Italian mathematician Giovanni Ceva (ˈtʃeva, CHAY-va), who proved it in 1678. But as usual in mathematics the theorem is not named for the original discoverer. That was Abu Amir Yusuf ibn Ahmad ibn Hud, who proved it in the 11th century. (I got the above proof from this website, though I have cut some corners by ignoring signed distances and neglecting the case with an obtuse triangle.)

Given Ceva's theorem, we can trivially prove that the medians of a triangle are concurrent. The midpoints divide each side in the ratio 1/1, so

1/1 * 1/1 * 1/1 = 1

proves the existence of the centroid. There are much more direct ways to prove this, of course, but Ceva's theorem will come up over and over again in the study of triangles so it's worthwhile to get it down now.

Now since we've proved that the medians are coincident, here are some of the properties of the medians and centroid.

The medians divide the triangle into six triangles of equal area.

Each median divides the triangle into two triangles of equal area, because they have equal bases and heights. Therefore

T+U+V = X+Y+Z

but also

Z+T+U = V+X+Y

and subtracting the second from first gives

V-Z = Z-V

V = Z

and similarly for every pair of opposite triangles. But also, X and V have equal bases and heights, so X = V, similarly T = U, Y = Z. Putting that all together shows that all six areas are equal.

The centroid G divides the triangle ABC into three triangles ABG, BCG, and ACG of equal area.

This follows immediately from the previous result, and we can immediately follow that with

The centroid lies on each median at 2/3 of the distance from a vertex to a midpoint.

ABG has the same base as ABC, and 1/3 the area, so it must have 1/3 the height. Those two very straightforward facts give us this less obvious property:

A point X divides a triangle ABC into equal triangles ABX, BCX, and ACX only if X is the centroid.

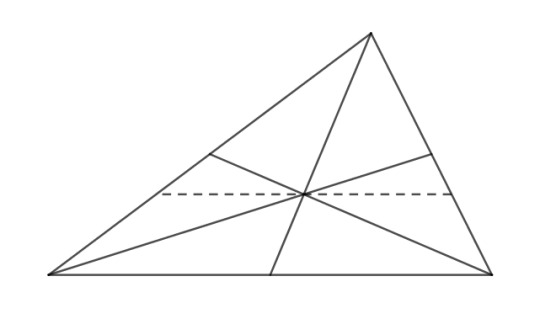
For a triangle ABX to have 1/3 the area of ABC, it must have a height 1/3 that of ABC, so X must lie on the dotted line in the picture, which runs through G. Analogous lines for triangles BCX and ACX must also concur at G.

And, of course, the most famous properties of the centroid, and the reason G is traditionally used to name it, are that the centroid is the center of gravity of the vertices, and also of the area of the triangle. (If you are coming from a physics background, you might object that the centroid of an object is by definition its center of gravity, or center of mass -- that's simply what "centroid" means. To avoid any confusion, I am using a gemometric definition of centroid as the place where the medians cross, and proving that this point is also the center of gravity.)

The centroid is the center of gravity of the vertices.

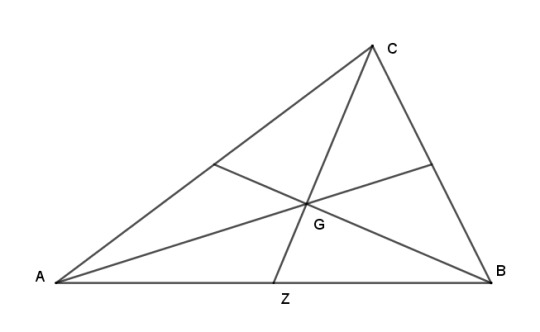
If A and B represent equal masses M, they can be replaced by a single mass of 2M located at Z. The center of gravity of C and Z, then, is a point 1/3 of the way from Z to C, which is G.

The centroid is the center of gravity of the area of the triangle.

Every line parallel to AB can be replaced with a mass Z_1, Z_2, ... at the midpoint of the line. Each of these masses will be located on the median, and so the center of gravity of all these points must also lie on the median. By a similar argument, the center of mass must also line on the other medians, so it must lie at their crossing point. (Yes I admit this is rather handwavy, but a better proof requires integration and I am doing elementary geometry here, not calculus. I have an idea for a proof using purely geometrical methods but I haven't finished it.)

To be complete, I will note that the centroid is not the center of gravity of the perimeter of the triangle. That's a different triangle center, which we will perhaps consider on a different day.

Finally let me introduce two triangles related to the centroid and the medians. The medial triangle, shown in red, is the triangle formed by the midpoints of the sides. The antimedial triangle, shown in blue, formed by lines passing through the vertices A, B, and C and parallel to the opposite side, which meet at A', B', and C'. The anti- part comes from the fact that ABC is the medial triangle of A'B'C.

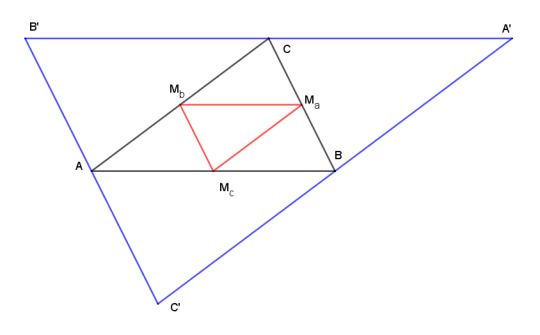
Both of these new triangles are similar to the reference triangle ABC and can be formed by reflecting ABC through a point and scaling up or down by a factor of 2. That point of reflection is, of course, the centroid.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[coraniaid]

top 5 mathematical identities :)

I wish Tumblr supported LaTeX.

OK, not trying to overthink this too much.

There are lots of fun identities involving binomial coefficients (or their q-analogs), or related integer sequences like the Catalan numbers and Motzkin numbers. But I think I have to go with the Chu-Vandermonde identity: who doesn't like a good convolution formula?

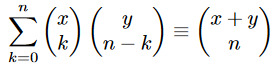
Of all the trigonometric identities I've ever had to learn, this is certainly not the most useful in practice or the hardest to prove or, arguably. the most inherently interesting either. I think the half-angle formula for tan is surprisingly pretty though.

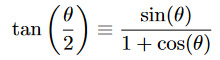
Let S be a finite set of real numbers. The maximum-minimums identity relates the largest element of this set to the smallest elements of every (non-empty) subset of S.

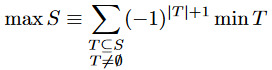
or, more concretely,

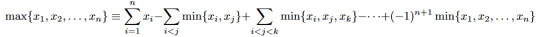
Perhaps not classically beautiful, but certainly enormously useful, the Sherman-Morrisson-Woodbury identity in linear algebra gives a formula for computing the inverse of a rank-k update of an invertible matrix by doing rank-k updates of the inverse of that original matrix. It's valid whenever the matrices are suitably conformable and when both the required inverses exist.

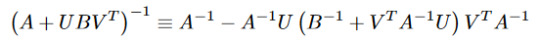
I feel like I have to include something due to Euler here, but -- rather than one of the famous ones involving π or anything to do with topology -- I'll go with some analytic number theory. The pentagonal number theorem gives a series expansion of the Euler function, valid for any complex x in the unit circle.

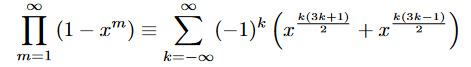
or, expanding both sides,

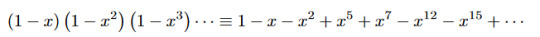
That takes us into the world of q-series and we can generalize it further to get Jacobi's triple product formula or various identities due to Ramanujan or MacDonald's identities for affine root systems or other increasingly exotic and strange things ... but this identity is the prototype for all of them.

[jonathankatwhatever]

It’s 25 May 2024, and I’m a little confused. I started to think about coprimes and Dirichlet’s progressions and how the theorem for that gets into L-functions, which are analytic continuations in which the case of 1 is the zeta series and function, the difference being the latter implies functional equation and an Euler product, which is notation for the infinite product of one of those progressions. We know the Riemann material and can explain the ½ real part in great depth. So why can’t I understand from that End to the coprime End? The idea is to describe the structure this generates, which every fibre says constructs 1Space to 0Space because this places 1Space 1’s in relation to whatever goes in within that 1.

Do you think there’s another way to say that there are 26 sporadic groups, maybe even 27, as a consequence of fCM? It’s only slightly less absurd to say there are 18 families of simple groups, countably infinite ones, because obviously that’s 2SBE3 and f&b. That they’re countably infinite makes it palatable. From our End, that is the reduction to what is necessary within gs Space for f&b, for 2SBE3 to functions, along with the other obvious counts which come together to create the necessary tensioning for dimensional existence.

I’m a little bit off today. This morning was really odd. I groggily got into coprimes and had a vision in which I could see the space between coprimes expanding. Then I asked if that made sense because what actually happens is you take coprimes and scale one to get a space and that space contains infinite primes. This made me question a vision, and those have never ever been wrong. I even went over that: when was the last time something which came to you in that manner, about mathematics, was wrong? Never. So what did I see?

Maybe I should continue and see if something comes. I then had a series of deep revelations that I assume will come back to me because the concept of coprime means no common factors, which means distinct or discrete gs Things, so the relationship between them, when one is scaled, generates gs primes. Not there yet.

I forgot to take a pill while drinking milk. This could be bad. Just swallowed two pills. Hope it’s not too late.

First, remember that it isn’t every combination that works as a progression. Then, try to visualize how this becomes I//I because the generation in gs requires the compositing of Irreducible layers. That says we define an Irreducibility between 2 numbers, and then scale that. And when we scale that in specific ways, it generates through the same compositing the same bip pole. Getting there.

Oh, Storyline has advanced tremendously. G and J are now at the stage where they have a straight conversation and I heard J say on my walk here that she modeled a shell which contracts to a point and a point that expands to a shell, with each being to all but the label. G gets that. They’re communicating very well. So the exchange of labels, of perspective labels, occurs in the contraction/expansion, which is to to the point, which is also to the ‘point’ of the object’s shell, so those have to match. See the mechanism? Oh come on, you can get this.

I think I just realized how nuts you are. This material is absurdly advanced. Help.

So they matchy match. Which is a form of coprime. Scale one. Scale into a specific progression that generates gs primes because it can so it does in 1Space. Okay. Mutuality of commitment and the like. Okay. Weird how that kind of display connects here. Makes sense but still.

Inversion. I forgot about smallness. Not really because the zeta series and L-functions are within CM1. Thus the divergence beyond. That’s super crucial to the basic conception of gsSpace, that it constructs within and outside. I want to say without to be cool but it doesn’t work because this is over Boundary.

Why reverse? So the internal identity checks complete. That’s amazing.

Need to take a break.

[jhavelikes]

We discuss some general aspects of renormalization group flows in four dimensions. Every such flow can be reinterpreted in terms of a spontaneously broken conformal symmetry. We analyze in detail the consequences of trace anomalies for the effective action of the Nambu-Goldstone boson of broken conformal symmetry. While the c-anomaly is algebraically trivial, the a-anomaly is "non-Abelian," and leads to a positive-definite universal contribution to the S-matrix of 2->2 dilaton scattering. Unitarity of the S-matrix results in a monotonically decreasing function that interpolates between the Euler anomalies in the ultraviolet and the infrared, thereby establishing the a-theorem.

[1107.3987] On Renormalization Group Flows in Four Dimensions

[fulltestbank]

Test Bank For Elementary Differential Equations and Boundary Value Problems, 12th Edition  William E. Boyce

TABLE OF CONTENTS   Preface v   1 Introduction 1   1.1 Some Basic Mathematical Models; Direction Fields 1   1.2 Solutions of Some Differential Equations 9   1.3 Classification of Differential Equations 17   2 First-Order Differential Equations 26   2.1 Linear Differential Equations; Method of Integrating Factors 26   2.2 Separable Differential Equations 34   2.3 Modeling with First-Order Differential Equations 41   2.4 Differences Between Linear and Nonlinear Differential Equations 53   2.5 Autonomous Differential Equations and Population Dynamics 61   2.6 Exact Differential Equations and Integrating Factors 72   2.7 Numerical Approximations: Euler’s Method 78   2.8 The Existence and Uniqueness Theorem 86   2.9 First-Order Difference Equations 93   3 Second-Order Linear Differential Equations 106   3.1 Homogeneous Differential Equations with Constant Coefficients 106   3.2 Solutions of Linear Homogeneous Equations; the Wronskian 113   3.3 Complex Roots of the Characteristic Equation 123   3.4 Repeated Roots; Reduction of Order 130   3.5 Nonhomogeneous Equations; Method of Undetermined Coefficients 136   3.6 Variation of Parameters 145   3.7 Mechanical and Electrical Vibrations 150   3.8 Forced Periodic Vibrations 161   4 Higher-Order Linear Differential Equations 173   4.1 General Theory of n?? Order Linear Differential Equations 173   4.2 Homogeneous Differential Equations with Constant Coefficients 178   4.3 The Method of Undetermined Coefficients 185   4.4 The Method of Variation of Parameters 189   5 Series Solutions of Second-Order Linear Equations 194   5.1 Review of Power Series 194   5.2 Series Solutions Near an Ordinary Point, Part I 200   5.3 Series Solutions Near an Ordinary Point, Part II 209   5.4 Euler Equations; Regular Singular Points 215   5.5 Series Solutions Near a Regular Singular Point, Part I 224   5.6 Series Solutions Near a Regular Singular Point, Part II 228   5.7 Bessel’s Equation 235   6 The Laplace Transform 247   6.1 Definition of the Laplace Transform 247   6.2 Solution of Initial Value Problems 254   6.3 Step Functions 263   6.4 Differential Equations with Discontinuous Forcing Functions 270   6.5 Impulse Functions 275   6.6 The Convolution Integral 280   7 Systems of First-Order Linear Equations 288   7.1 Introduction 288   7.2 Matrices 293   7.3 Systems of Linear Algebraic Equations; Linear Independence, Eigenvalues, Eigenvectors 301   7.4 Basic Theory of Systems of First-Order Linear Equations 311   7.5 Homogeneous Linear Systems with Constant Coefficients 315   7.6 Complex-Valued Eigenvalues 325   7.7 Fundamental Matrices 335   7.8 Repeated Eigenvalues 342   7.9 Nonhomogeneous Linear Systems 351   8 Numerical Methods 363   8.1 The Euler or Tangent Line Method 363   8.2 Improvements on the Euler Method 372   8.3 The Runge-Kutta Method 376   8.4 Multistep Methods 380   8.5 Systems of First-Order Equations 385   8.6 More on Errors; Stability 387   9 Nonlinear Differential Equations and Stability 400   9.1 The Phase Plane: Linear Systems 400   9.2 Autonomous Systems and Stability 410 9.3 Locally Linear Systems 419   9.4 Competing Species 429   9.5 Predator – Prey Equations 439   9.6 Liapunov’s Second Method 446   9.7 Periodic Solutions and Limit Cycles 455   9.8 Chaos and Strange Attractors: The Lorenz Equations 465   10 Partial Differential Equations and Fourier Series 476   10.1 Two-Point Boundary Value Problems 476   10.2 Fourier Series 482   10.3 The Fourier Convergence Theorem 490   10.4 Even and Odd Functions 495   10.5 Separation of Variables; Heat Conduction in a Rod 501   10.6 Other Heat Conduction Problems 508   10.7 The Wave Equation: Vibrations of an Elastic String 516   10.8 Laplace’s Equation 527   A Appendix 537   B Appendix 541   11 Boundary Value Problems and Stur-Liouville Theory 544   11.1 The Occurrence of Two-Point Boundary Value Problems 544   11.2 Sturm-Liouville Boundary Value Problems 550   11.3 Nonhomogeneous Boundary Value Problems 561   11.4 Singular Sturm-Liouville Problems 572   11.5 Further Remarks on the Method of Separation of Variables: A Bessel Series Expansion 578   11.6 Series of Orthogonal Functions: Mean Convergence 582   Answers to Problems 591   Index 624         Read the full article

[rbrooksdesign]

MPS, #13, 05-13, 2022, Reginald Brooks

∑ = running sum

PN = Perfect Number = xz

Mp = Mersenne Prime = z = 2ᵖ - 1 = x + y

Mp² = Mersenne Prime Square = MPS = z²

x = 2ᵖ⁻¹ = short side of PN rectangle

y = x-1 = short side of OC rectangle

OC = ODD Complement rectangle to PN = yz

Mp² = PN + OC = xz + yz = z²

CR = Complement Rectangle = xy

2ⁿ = exponential power of 2, where n = 1,2,3,…, e.i. 2ⁿ = 1–2–4–8–16…

∑ of 2ⁿ = 1–3–7–15–31–…, the difference (∆) = 2–4–8–16–..

x² = Perfect Number Square

1_2_4_8_16_32_64_128_256_512_1024_… —The Butterfly Fractal 1 — defines the Mersenne Prime-Perfect Number relationship.

If you take a Perfect Number (PN) — which is always EVEN — and sequentially divided it by two, it will always land on an ODD number known as a Mersenne Prime (Mp). Euclid — and later, Euler — knew about this and expressed it as the Euclid-Euler Theorem.

That PN ÷ by some number of twos = Mp. The Euclid-Euler Theorem states that formally as an algebraic equation:

PN = 2ᵖ⁻¹ (2ᵖ -1)

where p = prime, 2ᵖ -1 = Mp and 2ᵖ⁻¹ is another way of saying 2ⁿ (where n=1,2,3,..), i.e. how many doublings of two times the Mersenne Prime = the Perfect Number. This works, if and only if, 2ᵖ -1 = Mp, e.i. if p=11, a prime, but 2¹¹ -1 is not a Mp, there is no PN generated.

2ⁿ is the expression for the exponential power of 2, where 2^0 = 1, 2¹ = 2, 2² = 4, 2³ = 8… Do notice that 2ᵖ⁻¹ always solves to some form of 2ⁿ, e.i. 2^( 7-1) = 2⁶ = 64 as p=ODD and subtracting 1 from an ODD = EVEN.

In my installation, “The MPS Project,” in Building 5 in July of 2021, I showed visually why this is true as the new geometry extension of this Euclid-Euler Theorem plays out: namely, that squaring the Mp (treated as a “long” side) to give a geometric Square — Mersenne Prime Square (MPS) — contains within itself two Rectangles, one being the PN, the other its ODD Complement (OC). (The PN has a “short” side = x, the OC = y, with y = x-1 and x + y = z = Mp.)

If you take that PN Rectangle and sequentially diminish it by half (divide by two over and over) until it reaches an ODD, that ODD = the Mersenne Prime (Mp, as 1 x the side of that PN Rectangle).

While symmetry prevails, the center defines!

[uuuuuhhhhhhhhhhhhhhhhhh]

When banned from using "trivially" in a proof...

“Hello all. In a fellow mathposter's topology class they were not allowed to use the word "trivially" or any synonym thereof his proofs. The person presenting his work then crossed out "trivially" and wrote instead "indubitably." This inspired him to write a program that will insert condescending adverbial phrases before any statement in a math proof. Trivially, this is a repost. Below is the list--please come up with more if you can!

Obviously

Clearly

Anyone can see that

Trivially

Indubitably

It follows that

Evidently

By basic applications of previously proven lemmas,

The proof is left to the reader that

It goes without saying that

Consequently

By immediate consequence,

Of course

But then again

By symmetry

Without loss of generality,

Anyone with a fifth grade education can see that

I would wager 5 dollars that

By the contrapositive

We need not waste ink in proving that

By Euler

By Fermat

By a simple diagonalization argument,

We all agree that

It would be absurd to deny that

Unquestionably,

Indisputably,

It is plain to see that

It would be embarrassing to miss the fact that

It would be an insult to my time and yours to prove that

Any cretin with half a brain could see that

By Fermat’s Last Theorem,

By the Axiom of Choice,

It is equivalent to the Riemann Hypothesis that

By a simple counting argument,

Simply put,

One’s mind immediately leaps to the conclusion that

By contradiction,

I shudder to think of the poor soul who denies that

It is readily apparent to the casual observer that

With p < 5% we conclude that

It follows from the Zermelo-Fraenkel axioms that

Set theory tells us that

Divine inspiration reveals to us that

Patently,

Needless to say,

By logic

By the Laws of Mathematics

By all means,

With probability 1,

Who could deny that

Assuming the Continuum Hypothesis,

Galois died in order to show us that

There is a marvellous proof (which is too long to write here) that

We proved in class that

Our friends over at Harvard recently discovered that

It is straightforward to show that

By definition,

By a simple assumption,

It is easy to see that

Even you would be able to see that

Everybody knows that

I don’t know why anybody would ask, but

Between you and me,

Unless you accept Gödel’s Incompleteness Theorem,

A reliable source has told me

It is a matter of simple arithmetic to show that

Beyond a shadow of a doubt,

When we view this problem as an undecidable residue class whose elements are universal DAGs, we see that

You and I both know that

And there you have it,

And as easy as ABC,

And then as quick as a wink,

If you’ve been paying attention you’d realize that

By the Pigeonhole Principle

By circular reasoning we see that

When we make the necessary and sufficient assumptions,

It is beyond the scope of this course to prove that

Only idealogues and sycophants would debate whether

It is an unfortunately common misconception to doubt that

By petitio principii, we assert that

We may take for granted that

For legal reasons I am required to disclose that

It is elementary to show that

I don’t remember why, but you’ll have to trust me that

Following the logical steps, we might conclude

We are all but forced to see that

By the same logic,

I’m not even going to bother to prove that

By Kant’s Categorical imperative,

Everyone and their mother can see that

A child could tell you that

It baffles me that you haven’t already realized that

Notice then that

Just this once I will admit to you that

Using the proper mindset one sees that

Remember the basic laws of common sense:

There is a lovely little argument that shows that

Figure 2 (not shown here) makes it clear that

Alas, would that it were not true that

If I’m being honest with you,

According to the pointy-headed theorists sitting in their Ivory Towers in academia,

We will take as an axiom that

Accept for the moment that

These are your words, not mine, but

A little birdie told me that

I heard through the grapevine that

In the realm of constructive mathematics,

It is a theorem from classical analysis that

Life is too short to prove that

A consequence of IUT is that

As practitioners are generally aware,

It is commonly understood that

As the reader is no doubt cognizant,

As an exercise for the reader, show that

All the cool kids know that

It is not difficult to see that

Terry Tao told me in a personal email that

Behold,

Verify that

In particular,

Moreover,

Yea verily

By inspection,

A trivial but tedious calculation shows that

Suppose by way of contradiction that

By a known theorem,

Henceforth

Recall that

Wherefore said He unto them,

It is the will of the Gods that

It transpires that

We find

As must be obvious to the meanest intellect,

It pleases the symmetry of the world that

Accordingly,

If there be any justice in the world,

It is a matter of fact that

It can be shown that

Implicitly, then

Ipso facto

Which leads us to the conclusion that

Which is to say

That is,

The force of deductive logic then drives one to the conclusion that

Whereafter we find

Assuming the reader’s intellect approaches that of the writer, it should be obvious that

Ergo

With God as my witness,

As a great man once told me,

One would be hard-pressed to disprove that

Even an applied mathematician would concede that

One sees in a trice that

You can convince yourself that

Mama always told me

I know it, you know it, everybody knows that

Even the most incompetent T.A. could see,

This won't be on the test, but

Take it from me,

Axiomatically,

Naturally,

A cursory glance reveals that

As luck would have it,

Through the careful use of common sense,

By the standard argument,

I hope I don’t need to explain that

According to prophecy,

Only a fool would deny that

It is almost obvious that

By method of thinking,

Through sheer force of will,

Intuitively,

I’m sure I don’t need to tell you that

You of all people should realize that

The Math Gods demand that

The clever student will notice

An astute reader will have noticed that

It was once revealed to me in a dream that

Even my grandma knows that

Unless something is horribly wrong,

And now we have all we need to show that

If you use math, you can see that

It holds vacuously that

Now check this out:

Barring causality breakdown, clearly

We don't want to deprive the reader of the joy of discovering for themselves why

One of the Bernoullis probably showed that

Somebody once told me

By extrapolation,

Categorically,

If the reader is sufficiently alert, they will notice that

It’s hard not to prove that

The sophisticated reader will realize that

In this context,

It was Lebesque who first asked whether

As is tradition,

According to local folklore,

We hold these truths to be self-evident that

By simple induction,

In case you weren’t paying attention,

A poor student or a particularly clever dog will realize immediately that

Every student brought up in the American education system is told that

Most experts agree that

Sober readers see that

And would you look at that:

And lo!

By abstract nonsense,

I leave the proof to the suspicious reader that

When one stares at the equations they immediately rearrange themselves to show that

This behooves you to state that

Therefore

The heralds shall sing for generations hence that

If I’ve said it once I’ve said it a thousand times,

Our forefathers built this country on the proposition that

My father told me, and his father before that, and his before that, that

As sure as the sun will rise again tomorrow morning,

The burden of proof is on my opponents to disprove that

If you ask me,

I didn’t think I would have to spell this out, but

For all we know,

Promise me you won’t tell mom, but

It would be a disservice to human intelligence to deny that

Proof of the following has been intentially omitted:

here isn’t enough space in the footnote section to prove that

Someone of your status would understand that

It would stand to reason that

Ostensibly,

The hatred of 10,000 years ensures that

There isn’t enough space in the footnote section to prove that

Simple deduction from peano’s axioms shows

By a careful change of basis we see that

Using Conway’s notation we see that

The TL;DR is that

Certainly,

Surely

An early theorem of Gauss shows that

An English major could deduce that

And Jesus said to his Apostles,

This fact may follow obviously from a theorem, but it's not obvious which theorem you're using:

Word on the streets is that

Assuming an arbitrary alignment of planets, astrology tells us

The voices insist that

Someone whispered to me on the subway yesterday that

For surely all cases,

Indeed,

(To be continued)

[art-of-mathematics]

I made this collage many years ago - called it "Theory of Everything".

Infodumping:

The guy in the middle is Edward Frenkel (I literally forgot his full name, I knew he was called Edward Fra/enk... and then I couldn't remember... ) but he's one of my idols. Plus he wrote about the Langland's program, which is like the unified/ theory of everything in the math field. Also he is a human of value, as I have read in his autobiography "Love and Math" (which I sadly never finished, because so much thoughts and literally too few time to analyze everything til the end.)

The green thingy in the top right is a Lorentz attractor. (Sidenote: I have huge issues with left and right distinction, because my brain also thinks "reversely"/ mirrored, plus my dissociative mind tends to see me from above and what the fuck, do you mean this left or the left I see when I rotate my view by 180 degrees?)

The entire piece consists of chaos nd portrays my mind. (Secret order is hidden.) Intuitive paths...

The main parts are tesseract-nets, 3-dimensional nets of a four-dimensional cube, or hypercube/tesseract.

Quantum foam included! This word was introduced by John A. Wheeler as he tried to describe the immense activities on the quantum scale. Cool thing is: it, say rhe spacetime net, *appears* smooth at the first look, but if you zoom into it, it will look like "foam", chaos intensifies!

This brings me to the concept that all pure deterministic values (1 OR 0) are a product of a superordinated probabilistic system as proposed in Quantum mechanics (procentual probabilities, like 1 AND 0). A probabilistic system gets deterministic if observed/interacted with. Leads to wave function collapse. The wave function collapse is a prduct of a cross-section of the wave function, so to speak.

This leads to "Euler's identity: a formula that describes that cosine and sine are just 2-dimensional pictures of the 3-dimensional helix.

Also: what came first: Natural, imaginary or real numbers?

My solution for a theory of everything: Trying to make General Relativity fit with Quantum Mechanucs on the SAME LEVEL is line comparing apples with apple trees... you see what I mean: one thing is sub-ordinated, the other superordinated, one thing is nested onto the other...

Leads to ideas regarding recursion and furthermore self-reference combined with thoughts bout Gödel's Incompleteness.. (That's gives it a whole new level...*pun intended*)

Fractal pattern, fractal dimensions and dimensions in general. A dimension is just how much dots (0-D) are connected: 1D: the line (1 dot has one connection to another dot), 2D: the square (one dot has 2 connections to another dots), 3D: the cube (one dot has 3 connections); 4D: the hypercube (one dot has 4 connections to other dots)... yoz see a pattern?

Leads indirectly to quaternions and other hypercomplex number systems...

Relation to Platonic solids? Paterns of three, (the tetrahedron, octahedron and icosahedron), four (cube) and five (dodecahedron)

Data science/ statistics side thought - everything is just mathematical information. Physical reality is embedded in Mathematical reality, and is the rounded version of the infinitely complex Mathematical reality. Loops to the thought of wave function. Something is just *real* if it interacts, otherwise it's everywhere and nowhere simultaneously. Hence if it interacts it needs to be "rounded" aka the probabilities need to simiplify themselves.

Side note to Synergetics (After Buckminster Fuller after whom the C60-molecule "Bucky-ball" is named: regarded as geometry of thinking; and after Hermann Haken, (who is still alive and almost 100yo and lives in Stuttgart currently and was born in Leipzig, just 150km away from where I live.): acoording to Haken, Synergetics is the study of interaction. One important upshot: microscopic chaos creates macroscopic order. ...backloop to my idea about deterministic and probabilistic systems (equivalent)

Utter amazement of this terribly chaotic stream of thoughts... that's when you think recursively AND self-referently... i am just imitating the logic of the universe... a living paradox whose only escape is the meta level (reference to implications of gödel's incompleteness theorems)...

Whatever. I have head aches now.

That was intense brain storming...

And keep in mind:

Speculation and skepticism are both the key to theoretical discoveries.

(Inconsistent ideas get transformed/ erased.)

This thought stream is literally the upshot of my now already 9 years old hypothesis, or some few key concepts...

[positively-knotted]

Thom Isomorphism & the Euler Class

As promised, another longpost. This one might be a bit more technical than others I've done recently, but hopefully still approachable to someone who's done a reasonable course in algebraic topology (Ch 1-3 of Hatcher) and also knows what a fibre/vector bundle is. The end goal will be to introduce the Euler class as a generalisation of the Euler characteristic, and to motivate characteristic classes more generally.

A Brief Note on Vector Bundles

It's always difficult to know where to start with these things, but let's assume that you know what a vector bundle is, and that I don't have to motivate working with them. In case you've only seen them for manifolds before, observe that the definition works just as well for any reasonably nice space - I'll assume everything is a CW complex, although CW approximation means I don't actually have to.

A more interesting idea is this. To any manifold M, we have a canonical vector bundle TM, the tangent bundle. So if something is a property of manifolds, we can ask whether it is actually a property of TM, and if so, can it be generalised to other vector bundles? Suprisingly the answer is often yes.

The Leray-Hirsch Theorem

I can't prove everything, so let's state a theorem that we'll use later. Ignore the theorem numbering, and cohomology is taken with R-coefficients.

You should think of this as a version of the Kunneth theorem, that generalises from products to more general fibre bundles. Condition (i) is just a rephrasing of the vanishing of the Tor term - like the in the Kunneth theorem, it's automatic if we take R to be a field. (ii) is a niceness condition on the bundle, and it's a good exercise to check that it will be satisfied for a product.

I actually lied slightly, we're going to use a relative version of this. But like always in algtop, if you can believe the absolute version, you can believe the relative version.

The Thom Space

Suppose we have a rank n vector bundle π: E -> B. This is a bit annoying algebraically, because E homotopy retracts onto B no matter how twisted it is. So to capture any non-triviality we need to be a little bit clever. First, observe that we get a disc bundle π: D(E) -> B by just choosing a closed disc in fibre. (If we're in a manifold, choose a metric and take the unit disc. If we're not, you have to work a little harder to show this is well-defined). Now D(E) is a manifold with boundary, which is a sphere bundle S(E) -> B. Take the quotient D(E)/S(E) by collapsing the whole boundary to a point. We call this the Thom space T(E) of the vector bundle. Notice that T(E) is uniquely determined by π, but is definitely non-trivial!

As an example, take B= S^1, and consider the two line bundles. If E is the orientable line bundle, T(E) looks like a sphere with two points identified, so is homotopy equivalent to S^1 v S^2 [exercise]. If E is the non-orientable line bundle, then T(E) is RP^2.

You might notice that this is no longer a fibre bundle over B, as the point S(E)/S(E) lives in every "fibre". Oh well. It does have a nice CW decomposition though! First , give T(E) a single 0-cell, the point S(E)/S(E). Then suppose B has a fine enough decomposition that π is trivial over each cell [this is actually automatic, bc discs are contractible]. Each i-cell in B lifts to a (i+n)-disc in D(E), and under the quotient this is an (i+n)-cell in T(E). Like in my last post, you have to do a little bit of work to check that this really is a CW decomposition, but hopefully you believe me. You should double check with the line bundles over a circle that these do in fact give the usual cell structures.

Now, let's make the reasonable assumption that B is connected with a single 0-cell, so T(E) has one 0-cell, one n-cell, and no cells of dimension 1,...,n-1. Let's also suppose that π is R-oriented; that is, either the vector bundle is oriented and R is any ring, or it is unoriented and R = Z/2. Then the coboundary map of the n-cell to he (n+1)-cells is trivial [exercise: think about the boundary map from the 1-cells to the 0-cell in B]. In particular, H^n(T(E)) = R, and has a canonical generator coming from the choice of orientation! We call this the Thom class of E.

The Thom Isomorphism

More often, we work in relative cohomology, using the fact that

H^*(T(E)) = H^*(D(E), S(E)) = H^*(E,E\B).

Here the first isomorphism is the usual relative <--> quotient; the second is excision, and I'm identifying B with the 0-section. This is nice for the following reason. Given a choice of orientation, on each fibre F of E, we have a canonical generator of H^n(F, F\0). [This is possibly your definition of orientation, but if not then it's equivalent]. The Thom class is a class in H^n(E,E\B) that restricts to the generator on the fibre over the 0-cell. But the 0-cell was chosen arbitrarily, so in fact it restricts to the generator on every fibre! It's not obvious that such a class exists, so it's nice to see that it does.

Finally, let's apply the (relative) Leray-Hirsch theorem. H^i(F,F\0) is free for all i since F is just a vector space; condition (ii) is met by the Thom class! We can then make two final simplifications. Firstly, H^*(B) is isomorphic to H^*(E) by pulling back under π. Secondly, H^i(F,F\0) is either 0 or R, so vanishes in the tensor product. Putting it all together, we get the following.

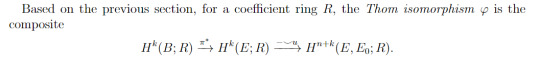
Phew! That's a lot of work, and we haven't even gotten to the Euler class yet.

The Euler Class

This is surprisingly easy. Remember that the Thom class lives in relative cohomology H^n(E,E\B). We can always pull back a relative class under inclusion to an absolute class u' ∈ H^n(E). Identifying this with H^n(B) again by π, we get the Euler class e(π) ∈ H^n(B)

Sometimes it's more helpful to think of it as follows. By the abstract nonsense that is the relative cup product, u⌣u = u'⌣u. So we get the following equivalent definition:

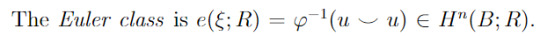
This can be nicer to work with, as u⌣u is a square so has some nice properties. For example, take the following basic facts:

(a) is true by checking that the Thom class pulls back - this follows directly from viewing it as the unique class restricting to the generator on fibres.

(b) is true by the same observation.

(c) is quite hard to prove using the first definition that we gave, but it follows directly from the fact that u⌣u = -u⌣u if n is odd. Note that this is a weaker version of the statement that the Euler characteristic of an odd dimensional manifold is 0!

(d) These are both actually kinda tricky, but it's not hard to convince yourself it's true.

Ok this post is already way too long, so I'll delay the main point until next time, when I'll link the Euler class to Poincare duality, and eventually to the actual Euler characteristic. For now, a teaser of why else it might be useful:

The first bullet follows directly from (c)+(d) above. For the second, suppose we had a nowhere-zero section s: B -> E\B. Writing i for the inclusion E\B -> E, we get the composite πis = id_B. But π^*e(π) = u' by definition, and i^* u' = 0 since u' is the pullback of a relative class! So e(π) = s^*(0) = 0.

As a sanity check for where we're going, recall that S^1 and S^3 have nowhere-zero vector fields while S^2 doesn't. The Euler characteristic of S^1 and S^3 is zero, while the Euler characteristic of S^2 is 2. This is looking promising!

[hondacivictrucknuts]

TLP (2013):

I don't want to be cynical, but boy oh boy is it hard not to observe that at the very moment in our history when we have the most women in the Senate, Congress is perceived to be pathetic, bickering, easily manipulated and powerless, and I'll risk the blowback and say that those are all stereotypes of women.  Easy, HuffPo, I know it's not causal, I am saying the reverse: that if some field keeps the trappings of power but loses actual power, women enter it in droves and men abandon it like the Roanoke Colony.

That sure sounds like academia!

I watched a Brett Weinstein “Dark Horse” podcast where he and his wife bemoaned the recent decision of the University of Chicago English department only to accept graduate applicants in Black Studies this cycle. This, at Chicago, of the Chicago Principles; one of the supposed bastions of academic freedom and open inquiry! But UofC is not a monolith: in 2008, a hundred-some faculty members signed this inane letter opposing the creation of the Milton Friedman Institute. The signatories include at least a dozen faculty of the English department, and that was 12 years ago (like everyone else, I know about this because of John Cochrane’s epic response). I, too, entered academia with idealistic (and obsolete) ideas about the rules of the academy and its role in society, so I can sympathize with Brett here, but the party is clearly over.

What problems do we face as a society, for which we look to academia for solutions? Our biggest problems do not appear likely to be solved by scientific breakthroughs or social scientific innovation. The most important legal innovation of the past few decades, originalism, was largely developed outside of the top Law departments; meanwhile, they gave us Critical Race Theory and Intersectionality. Twentieth century academic economists established the impossibility of communism and the advantages of free markets, giving a definitive answer to what had been a crucial open question at the end of World War 2. In the 1980s and 90s, they designed working markets for novel goods, like broadcast spectrum. What have they accomplished recently? Obamacare? Meanwhile many formerly serious economists have discovered the sweet treats of partisan hackery, from Paul Krugman to Justin Wolfers.

So it’s not bad news! Academia is an effective steam vent for passionate people of middling intellect, particularly women and minorities, who might cause trouble if allowed into the real spheres of power. And we have enough books and theorems for now, so it doesn’t matter if progress stalls in most fields. Seriously, I remember seeing evidence that “even mathematics!” was becoming woke, but it’s not like there’s a modern-day Longitude Problem that tomorrow’s (white, male) Leonard Euler will be prevented from solving. I trust that in mathematics, and in all fields, enough passionate people will keep alive the intellectual tradition necessary to read the old books, and as our social needs shift back towards scientific breakthroughs they will teach the next generation.

So, where has the innovation moved to? Where are all the creative and intelligent men now? One obvious answer is podcasting, sadly. And various other online platforms. There are some clever guys in manufacturing. I guess we’ll see!

[astronomerosh19]

Differential equations have been a major branch of pure and applied mathematics since their inauguration in the mid 17th century. Differential equations' began with Leibniz, the Bernoulli brothers, and others from the 1680s, not long after Newton's `fluxional equations' in the 1670s. Applications were made largely to geometry and mechanics; isoperimetrical problems were exercises in optimisation. Most 18th-century developments consolidated the Leibnizian tradition, extending its multi-variate form, thus leading to partial differential equations. Generalisation of isoperimetrical problems led to the calculus of variations. New figures appeared, especially Euler, Daniel Bernoulli, Lagrange, and Laplace. Development of the general theory of solutions included singular ones, functional solutions, and those by infinite series. Many applications were made to mechanics, especially to astronomy and continuous media. In the 19th century: general theory was enriched by the development of the understanding of general and particular solutions, and of existence theorems. More types of the equation and their solutions appeared; for example, Fourier analysis and special functions. Among new figures, Cauchy stands out. Applications were now made not only to classical mechanics but also to heat theory, optics, electricity, and magnetism, especially with the impact of Maxwell. Later Poincaré introduced recurrence theorems, initially in connection with the three-body problem. In the 20th century: general theory was influenced by the arrival of set theory in mathematical analysis; with consequences for theorisation, including further topological aspects. New applications were made to quantum mathematics, dynamical systems, and relativity theory. #math #mathematics #equations #differential #leibniz #bernoulli #newton #geometry #mechanics #calculus #euler #theory #astronomy #astrophysics #cauchy #maxwell #poincaré #theorem #quantum #quantumphysics #physics #relativity #instagram #science #education #life #beautiful #quantummechanics #ordinary #instastudent ... 💫... https://www.instagram.com/p/B_yc2SsFTly/?igshid=xiirksitbub6

[jonathankatwhatever]

More on 21 August 2023. Hearing the same words intoned at me in childhood: you’re going to die. That preceded most of the big Storylines which began to appear after we broke apart at my tangible End. The segmenting isn’t intangible to physical but immediacy of the tangible.

That suggests I could abandon you here. Interesting because a few minutes ago, I saw a storyline in which you die and I publish and the use you to make it well known on the general sense. Not optimal but a storyline. I’ve never seen anything like that before. Leads to a whole set of negatives about you but not about you. Processes have byproducts.

Oh so a reversal of the ‘time’ process would be to immediate impact instead of from. That feels like D6 because there’s a pairing so 2 hats on a gs. And the 2 Irred forms. So ideal is from End to Start but that can’t happen so it forms what can and that appears in Hex.

What does it mean: can’t happen? Its gs construction: makes a ++ quadrant, finite existence, etc. That which is made.

By immediate impact, I mean if you knew all that would occur because of something that then happens, instead of something happening and the effects felt later.

That means D5 is that which enables permutation of D4 states, and this occurs within the D6 which contains as its outside edge the reversals. The other hat. This matches the concept we’ve used many times of a level including parts and those are separated, broken up.

Now it makes sense that the Euler numbers define the errors in digits which occur when you stop the series calculation so you catch the outside edge. They’re the inverse of the hyperbolic cosine. Which is the right ++ arm. This makes sense in D-structure because that means Boundary in πSquare is an HG and the hyperbolic fits to that. Contrary to appearance.

So HG is drawing in my head as defining a BT flipped over an End not a 1-0Seg. So it’s the expansion of and the link between 2 1-0Segs, as we’ve said many times. Oh, Riemann sphere and more. Point at infinity. The hairy ball theorem. I//I. So yeah, Boundary for HG does translate into a πSquare. It also says 2 Hexes are Attached so whatever works or processes through those is part of the Boundary of a Thing. Outer and Inner. OB and IB? Get a center Hex and thus IB and the attached fit to OB.

That is brilliant. Need a break.

[coursesforallacademynoida]

B.Tech Mathematics – I Back Paper Tuition In Noida

B.Tech Mathematics – I Back Paper Tuition In Noida

B.Tech Mathematics – I Back Paper Tuition In Noida

B.Tech Tuition In Noida, B.Tech Maths Tuition In Noida, B.Tech Tutors In Noida, B.Tech Subjects Coaching In Noida, B.Tech Back Paper Tuition In Noida, Best BTech Electronic & Communication Engineering Tutorial Classes, Best BTech Electrical & Electronic Engineering Tutorial Classes, Best BTech Mechanical Engineering Tutorial Classes, Best BTech…

[alukaforyou]

To be honest I would be kind of interested in seeing the paper that you have written for your math prof back then (you mentioned it somewhere (some time?) on Tumblr and on Instagram as well). I'd be interested in your opinion on math in general because I never would have thought that an amazing artist like you majored in math, it's very interesting to me. (Ignore if this all seems weird, LOL! I hope I haven't bothered you in any way.)

i didnt write a math paper i translated eulers e271 which was originally written in latin. it was abt one of fermat’s theorems and the totient function u can see the pdf here but its only in latin or a german translation! 

also im not majoring in math i go to an arts uni LOL i was just asking on insta story cuz i wanted to kno if any of my followers were math majors! i wanna say im good at certain kinds of math my mental arithmetic isnt too fast but idk if u explain it well i think i can do p okay. the prof who taught the course who i did the e271 for was soo amazing i understood everything!!

[comp6841]

The RSA Algorithm

Step 1: Picking Primes

The first step requires to choose two sufficiently large primes p and q - in practice these are usually 2048 bits, however 4096 bits would be on the safer side. I’m going to ignore the methods of secure random number generation here and assume that we are able to generate numbers of these length with sufficiently large entropy. Now we just have to check that each of the numbers we generate is a prime - if we have a look at the prime number theorem we’ll see that given a 4096 bit number we get the following:

So basically on average you will need to check 3076 numbers which are 4096 bits (assuming the most significant is always 1) before you find a prime. If you do the calculations but don’t make the assumption that the most significant bit is 1, you get a slightly higher percent approximation (around 0.035%ish) however this is only rough work here. To do this we usually utilise the Miller-Rabin test on p which involves the following:

Write p in the form p = 2^s*q+1 for some odd q

Pick an integer a in the range [2, p-1]

Calculate x = a^q (mod p)

If x = 1 or x = p - 1 then we say it is “probably prime”

Check a^(2^i) (mod n) = -1 for each integer i in the range [0, s-1]

If we can find such an i, then we say it is “probably prime”

If we get to the end here, then p is “composite”

By applying the Miller-Rabin test multiple times we can significantly reduce the probability - it turns out that the probability a composite number will pass the test is at most 1/4. So if we do 8 passes of Miller-Rabin then there is a maximum probability that it will actually be composite of 1/65536 - this would easily be sufficiently small enough for our purposes. The reason this is sufficient is because it is almost certain that the process of RSA will fail, if it is not prime, in decryption - this is because the algorithm is essentially a powerful primality test. I should probably mention as a sidenote that Miller-Rabin doesn’t detect Carmichael numbers:

Carmichael numbers satisfy the above property for all integers b coprime to n. These numbers can affect the security in RSA as some of their factors are relatively smaller - remember that the security in RSA rests on the fact that they are hard to factor. It’s important to note that they are relatively rare.

Specific Example: we will use the small primes 17 and 31 to demonstrate the algorithm.

Step 2: Calculate the value of n

Calculate n = p * q - this will be used as the modulus for the keys and will be available as part of the public key.

Specific Example: calculate n = 17 * 31 = 527

Step 3: Determine Euler’s totient function

We need to calculate Euler’s quotient ϕ(n)   = (p - 1) * (q - 1). This represents the number of positive integers that are relatively prime up to our integer n.

Specific Example: ϕ (n) = (17 - 1) * (31 - 1) = 480

Step 4: Calculate the encryption key e

In this part we need to find a number e that is coprime with ϕ(n) - this means that it doesn’t share any factors in the range [3,  ϕ(n)]. Interestingly enough, Fermat primes  (99% of the time) are almost always chosen for this such as 3, 5, 17, 257 and 65537. The reason being for this is that it is of the form F_n = 2^(2^n)+1 and as a result makes the calculations run a lot faster (without much of a significant setback in security). There are some attacks based on the Coppersmith Theorem available for using small values such as 3 as the encryption key, however they are far from a total break in security - paper on it here.

Specific Example: we will take the largest Fermat prime e = 257 in this case - this means our public key is the pairing (e = 257, n = 527)

Step 5: Determine the decryption key d

To find the decryption key we need to solve the equation d * e (mod ϕ) = 1, where d is the decryption key. We can utilise the Extended Euclidean algorithm to do this.

Specific example: we need to solve the equation d * 257 (mod 480) = 1 - we will do this via the Extended Euclidean Algorithm

So a solution to this equation is if we take d = 353. This means our private key pair is (d = 353, n = 527)

Step 6: Encrypting with the public key

The first thing we must do is convert the message into integer form - in the case of characters in a message we can just use their ASCII codes. Given a plaintext message m, we can then determine the ciphertext c with the formula c = m ^ e (mod n).

Specific Example: if we wanted to encrypt the letter ‘A’ then we would use the ASCII code of 65. So the ciphertext would be c = 65 ^ 257 (mod 527) = 456

Step 7: Decrypting with the private key

We convert the cipher text into an integer (if it isn’t already) then can determine the plaintext m = c ^ d (mod n). The reason this relationship works is due to the fact that (m^e)^d = m (mod n) - you can prove this result using either Fermat’s little theorem or Euler’s theorem (see here for proof).

Specific Example: we calculate the plaintext m = 456 ^ 353 (mod 527) = 65. This represents the letter ‘A’ in ASCII so we got our original result back